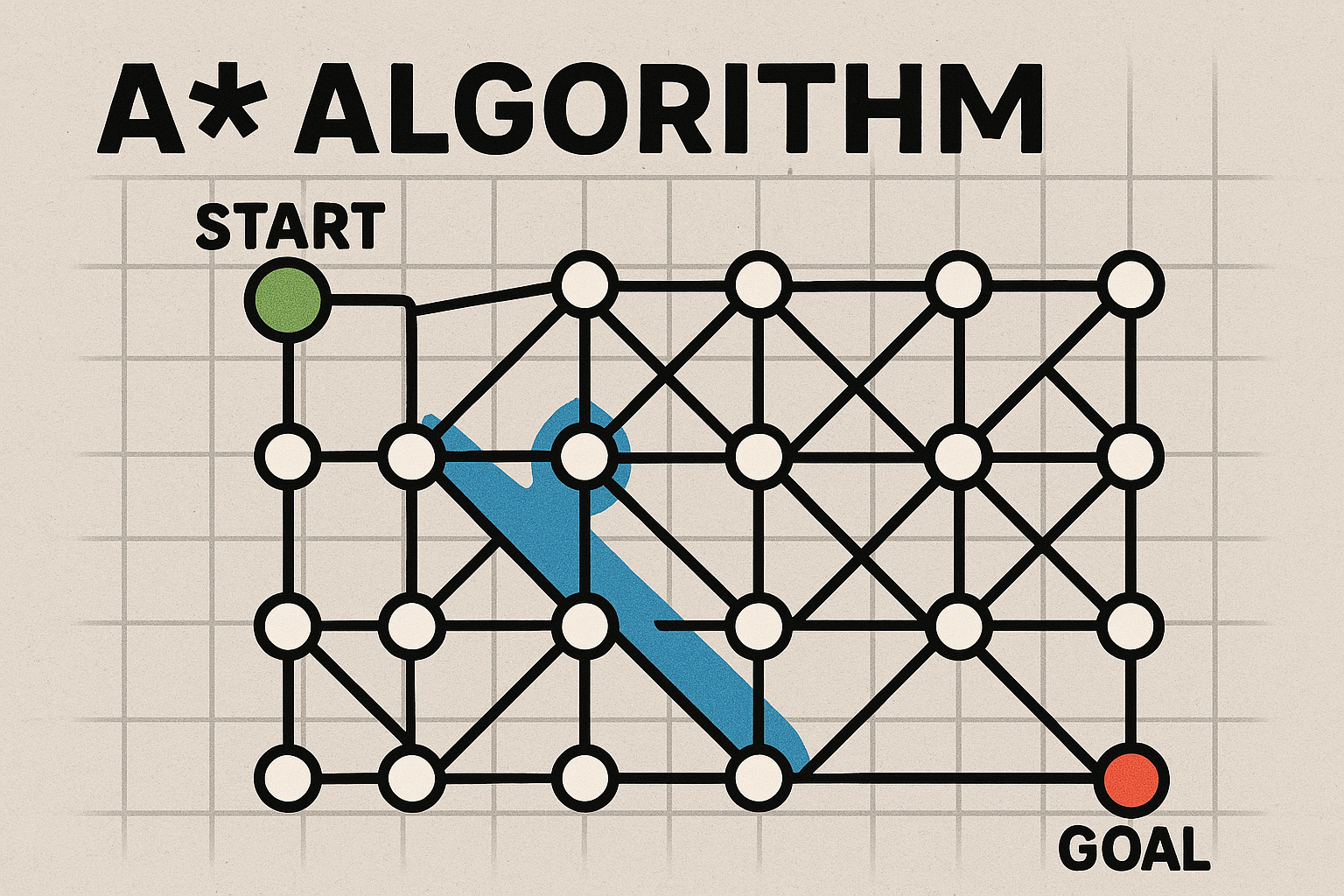
الگوریتم A* (ای-استار): مسیریابی هوشمند در بازی‌ها و نقشه‌ها 🗺️⚡

آیا تا به حال فکر کرده‌اید چرا شخصیت‌های بازی‌های رایانه‌ای به‌سرعت از موانع عبور می‌کنند؟ یا چرا اپلیکیشن‌های مسیریابی مثل گوگل مپس 🗺️ کوتاه‌ترین مسیر را پیشنهاد می‌دهند؟ پاسخ این سوالات در الگوریتم A* (ای-استار) نهفته است! این الگوریتم هوشمند، قلب تپنده سیستم‌های مسیریابی مدرن است و در این مقاله به طور ساده و جذاب با آن آشنا می‌شویم.

الگوریتم A* چیست؟ 🧠

A* یک الگوریتم جستجوی گراف است که برای یافتن کوتاه‌ترین مسیر بین دو نقطه (مثلاً نقطه شروع و هدف در نقشه) استفاده می‌شود. این الگوریتم با ترکیب دو روش قدرتمند، یعنی دایجسترا (تأکید بر هزینه قطعی) و جستجوی حریصانه (تأکید بر تخمین بهینه)، به یک راهکار سریع و دقیق دست یافته است.

فرمول جادویی A*: f(n) = g(n) + h(n) 🔢

• g(n): هزینه واقعی حرکت از نقطه شروع به نقطه فعلی.

• h(n): هزینه تخمینی (هیورستیک) از نقطه فعلی تا هدف.

• f(n): معیار کلی برای انتخاب گام بعدی.

الگوریتم A* همیشه گرهی را بررسی می‌کند که کمترین f(n) را دارد. این هوشمندی باعث می‌شود هم بهینه باشد (کوتاه‌ترین مسیر را پیدا کند) و هم سریع عمل کند!

چرا A* هوشمندانه‌تر است؟ 🚀

1. استفاده از هیورستیک: تخمین هوشمندانه h(n) (مثل فاصله اقلیدسی 📏 یا منهتن 🏙️) سرعت جستجو را افزایش می‌دهد.

2. بهینگی تضمینشده: اگر هیورستیک Admissible باشد (یعنی هرگز بیش‌ازحد واقعی تخمین نزند)، A* همیشه کوتاه‌ترین مسیر را پیدا می‌کند.

3. انعطاف‌پذیری: با تغییر تابع هیورستیک، می‌توان آن را برای محیط‌های مختلف (مثل بازی‌های سه‌بعدی یا نقشه‌های پیچیده) تنظیم کرد.

4.  

کاربردهای جذاب A* در دنیای واقعی 🎮

• بازی‌های رایانه‌ای: حرکت هوشمند کاراکترها در بازی‌هایی مثل Age of Empires یا Pac-Man.

• رباتیک: مسیریابی ربات‌های تحویل کالا در انبارها.

• اپلیکیشن‌های نقشه: محاسبه سریع‌ترین مسیر در Waze یا Google Maps.

• هوش مصنوعی: برنامه‌ریزی حرکتی در خودروهای خودران.

مزایا و محدودیت‌های A* ⚖️

✅ مزایا:

• سرعت بالا نسبت به دایجسترا.

• تضمین یافتن مسیر بهینه (با هیورستیک صحیح).

❌ محدودیت‌ها:

• مصرف حافظه بالا در محیط‌های پیچیده.

• وابستگی به دقت تابع هیورستیک.

نمونه کد ساده A* در پایتون 🖥️

python

import heapq

def astar(grid, start, end):
    # تعریف گره‌ها (ردیف, ستون) 🎯
    class Node:
        def __init__(self, pos, parent=None):
            self.pos = pos
            self.parent = parent
            self.g = 0  # هزینه واقعی تا این گره
            self.h = 0  # تخمین تا هدف
            self.f = 0  # مجموع g + h

        def __lt__(self, other):
            return self.f < other.f

    # توابع هیورستیک (فاصله منهتن) 📏
    def heuristic(a, b):
        return abs(a[0] - b[0]) + abs(a[1] - b[1])

    # لیست باز و بسته
    open_list = []
    closed_set = set()

    start_node = Node(start)
    end_node = Node(end)
    heapq.heappush(open_list, (0, start_node))

    while open_list:
        current = heapq.heappop(open_list)[1]
        closed_set.add(current.pos)

        # اگر به هدف رسیدیم 🎉
        if current.pos == end_node.pos:
            path = []
            while current:
                path.append(current.pos)
                current = current.parent
            return path[::-1]  # مسیر نهایی

        # تولید همسایه‌ها (بالا, پایین, چپ, راست) 🔄
        neighbors = [
            (current.pos[0]-1, current.pos[1]),
            (current.pos[0]+1, current.pos[1]),
            (current.pos[0], current.pos[1]-1),
            (current.pos[0], current.pos[1]+1)
        ]

        for neighbor in neighbors:
            # بررسی مرزهای شبکه و موانع ⛔
            if (neighbor[0] < 0 or neighbor[0] >= len(grid) or
                neighbor[1] < 0 or neighbor[1] >= len(grid[0]) or
                grid[neighbor[0]][neighbor[1]] == 1):
                continue

            new_node = Node(neighbor, current)
            new_node.g = current.g + 1
            new_node.h = heuristic(neighbor, end)
            new_node.f = new_node.g + new_node.h

            # اگر گره قبلاً بررسی شده
            if neighbor in closed_set:
                continue

            # افزودن به لیست باز
            heapq.heappush(open_list, (new_node.f, new_node))

    return None  # مسیر یافت نشد 😞

# مثال استفاده:
grid = [
    [0, 0, 0, 0],
    [0, 1, 1, 0],  # 1 = مانع
    [0, 0, 0, 0]
]
start = (0, 0)
end = (2, 3)
print("مسیر یافت شده:", astar(grid, start, end))  # خروجی: [(0,0), (0,1), (0,2), (1,3), (2,3)]

توضیح کد به زبان ساده 🧩

1. ساختار گره: هر گره موقعیت، والد، و هزینه‌ها (g, h, f) را ذخیره می‌کند.

2. لیست اولویت‌دار: گره‌ها بر اساس f(n) اولویت‌بندی می‌شوند.

3. تابع هیورستیک: در این مثال از فاصله منهتن استفاده شده (مناسب برای شبکه‌های شطرنجی).

4. جستجوی همسایه‌ها: ۴ جهت اصلی بررسی می‌شوند و موانع نادیده گرفته می‌شوند.

5. بازیابی مسیر: با دنبال کردن والد هر گره از انتها به شروع.

نکات طلایی برای توسعه‌دهندگان 💎

• برای محیط‌های سه‌بعدی، تابع هیورستیک را به فاصله اقلیدسی تغییر دهید.

• اگر مصرف حافظه مهم است، از ایندکس‌گذاری به جای ذخیره کل شی گره استفاده کنید.

• برای سرعت بیشتر، الگوریتم‌هایی مثل Jump Point Search را بررسی کنید.

جمع‌بندی: A*؛ قهرمان نامرئی مسیریابی! 🏆

الگوریتم A* با ترکیب هوشمندانه داده‌های واقعی و تخمین‌های بهینه، به یکی از محبوب‌ترین ابزارهای مسیریابی تبدیل شده است. چه در بازی‌ها، چه در نقشه‌های دیجیتال، این الگوریتم همچنان پایه‌گذار فناوری‌های پیشرفته آینده خواهد بود.

پس دفعه بعد که در بازی موبایلتان از دست دشمن فرار کردید یا نقشه، مسیر بدون ترافیک را پیشنهاد داد، بدانید A* در پس‌زمینه مشغول کار است! 💡